ESTÁTICA DOS FLUIDOS
O comportamento físico de uma partícula sólida pode ser representado e entendido facilmente porque ele constitui uma entidade única de tamanho suficiente e que podemos visualizar também o seu comportamento. Um sólido é uma substância rígida que conserva sua forma contra forças deformantes externas. Extensão das mesmas observações tornam-se mais complexas quando se trata com fluidos já que estamos, com efeito, tratando com uma coleção de partículas "virtuais" que não podem ser visualizadas. O termo fluido é usado para descrever um objeto ou substância que deve estar em movimento para resistir forças aplicadas externamente. Um fluido sempre escorre quando forças deformantes lhe são aplicadas. Note que embora a tendência é imaginar os fluidos principalmente como líquidos, os fluidos também descrevem o comportamento dos gases. Este capítulo apresenta os princípios físicos, conceitos e exemplos de um fluido em repouso (estática dos fluidos)e de um fluido em movimento (dinâmica dos fluidos). Estas propriedades aplicam-se tanto à passagem do ar através dos brônquios como à passagem do sangue através dos vasos sangüíneos.
4.1 – DEFINIÇÕES DE ESTÁTICA DOS FLUIDOS
4.1.1- DENSIDADE
A densidade r é uma propriedade física de um fluido, dada como massa por unidade de volume, ou
![]() ......vale para qualquer corpo
......vale para qualquer corpo
A densidade representa nos fluidos o equivalente à massa nos sólidos. Outras unidades usadas na prática são g/cm3 , kg/litro, etc. A sua dimensão é ML-3.
A densidade relativa de uma dada substância é a razão da densidade da substância r sub pela densidade da água r água, ou
densidade relativa = ![]()
EXEMPLO 1
Trinta mililitros de uma solução anestésica contida numa seringa de 5 g tem uma massa combinada de 80 g. Determine a densidade da solução anestésica,
SOLUÇÃO
A densidade da solução anestésica pode ser determinada de
![]()
onde r é a densidade (g/cm3), ma é a massa (g) da solução e V é o volume (cm3 ou ml). A massa da solução anestésica ma é a massa total mT menos aquela da seringa ms, ou
mT = ma + ms Þ ma = mT – ms = 80 – 5 = 75 g
O volume V da solução anestésica contida na seringa é
V = 30 ml = 30 cm3
Assim, a densidade de uma solução anestésica pode ser determinada por
r =
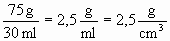
EXEMPLO 2
A densidade de um radiofármaco é 0,75 g cm-3. Determine a massa de 2,0 litros deste radiofármacoNota:- 1 litro = 1000 cm3
SOLUÇÃO
A massa de um líquido está relacionada à densidade e volume por
![]()
Rearranjando, e resolvendo para a massa m temos,
m = r V = (0,75 g cm-3) (2000cm3) = 1500 g = 1,5 kg.
EXEMPLO 3
Determine o tamanho apropriado de um recipiente necessário para manter 0,7 g de éter que tem uma densidade de 0,62 g . cm-3.
SOLUÇÃO
O volume de um líquido está relacionado à massa e a densidade por
V = m/r = (0,7 g)/(0,62 g cm-3) = 1,129 ml
EXEMPLO 4
Um cubo de alumínio sólido tem dimensões de 6 polegadas (6 in) de comprimento em cada lado. Dado que a densidade do alumínio é 170 lb ft-3, determine a sua massa. Dado : 1 pé = 1 ft = 12 in = 30,48 cm
SOLUÇÃO
Por definição, m = r . V. Sabemos também que 1 ft = 12 in. Então, O volume do cubo é:
V = 0,5 ft . 0,5 ft . 0,5 ft = 0,125 ft3
Portanto a massa é
m = (170 lb ft-3)(0,125 ft3) = 21,3 lb
EXEMPLO 5
O osso tem uma densidade de 1,06 g cm-3. Determine a densidade relativa do osso.
SOLUÇÃO
Por definição a densidade relativa é
densidade relativa =
=
EXEMPLO 6
Como calculado no problema prévio, a densidade relativa do osso é 1,06. Determine a massa de 1 cm3 de osso
SOLUÇÃO
A massa está relacionada à densidade relativa por
densidade relativa = 1,06 = 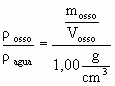 Þ
m = 1,06 g
Þ
m = 1,06 g
4.1.2 - PRESSÃO
A pressão P é definida como uma força F atuando
perpendicularmente a uma superfície de área A e é dada por
A pressão é uma quantidade escalar e é expressa em dimensões de ML-1T-2.
As unidades S.I. para pressão são Nm-2. Outras unidades são muito usadas na prática, a atmosfera (atm) e o milímetro de mercúrio (mmHg) e a "libra" (lb/in2).
EXEMPLO 7
Tocando um disco, uma agulha de fonógrafo exerce 3,5 g dentro de uma área circular de 0,30 mm de raio. Determine a pressão exercida pela agulha do fonógrafo no disco.SOLUÇÃO
A pressão exercida pela agulha do fonógrafo pode ser determinada da definição de pressão:
p = ![]()
Dois tipos específicos de pressão particularmente aplicável aos fluidos inclui pressão atmosférica e pressão hidrostática.
PRESSÃO ATMOSFÉRICA - representa a pressão média exercida pela atmosfera terrestre ao nível do mar e é definida numericamente como:
1 atm = 1,01 x 10 5 Nm-2 = 1,01 x 105 Pa = 760 mmHg .
Uma relação mais completa entre as várias unidades de pressão pode ser encontrada na Tabela 6.1
PRESSÃO HIDROSTÁTICA Phid - é a pressão de um fluido exercida numa profundidade h num fluido de densidade r e é dada por
Phid = r g h
Aqui g representa a aceleração da gravidade. Na medicina a unidade mais usada é o mmHg. Por exemplo, um pico de pressão sangüínea (sistólica) lida como 120 mmHg indica que uma coluna de mercúrio desta altura tem uma pressão na sua base igual a pressão sangüínea sistólica do paciente. Desde que a densidade do mercúrio é 13,6 g/cm3, uma coluna de água tem que ser 13,6 vezes maior que uma dada coluna de mercúrio, afim de produzir a mesma pressão. É algumas vezes conveniente indicar diferenças de pressão no corpo humano em termos da altura de uma coluna de água.
Se uma pressão externa Pext é exercida no fluido, então a pressão total P é a soma da pressão externa e da pressão hidrostática.
P = Pext + r g h
onde a pressão atmosférica, na maioria dos casos, é considerada uma pressão externa
Desde que vivemos num mar de ar com uma pressão de 1 atm, é mais fácil medir a pressão relativa à pressão atmosférica do que medir a verdadeira pressão, ou pressão absoluta. Assim quando dizemos que a pressão do pneu da bicicleta é 60 "libras" estamos falando do quanto temos além da atmosfera no pneu. Esta pressão "a mais" é chamada de pressão manométrica. A menos que falemos em contrário, todas as pressões usadas aqui são pressões manométricas.Existem vários lugares no corpo humano onde as pressões são mais baixas do que a atmosférica, ou negativas. Por exemplo quando inspiramos a pressão nos pulmões deve ser um pouco menor que a pressão atmosférica senão o ar não fluiria para dentro do corpo. Quando alguém bebe um líquido através de um canudo, a pressão na boca deve ser negativa por uma quantidade igual a altura da sua boca acima do nível do líquido que ele está bebendo. Para ver outros exemplos de pressão negativa clique aqui
EXEMPLO 8
A pressão sangüínea sistólica normal na circulação humana é de 120 mmHg. Determine a altura equivalente de uma coluna de água.SOLUÇÃO
Para determinar a pressão hidrostática exercida por uma coluna de mercúrio de 120 mm:
P = r g h = (13,6
Queremos agora determinar a altura de uma coluna de água requerida para exercer a mesma pressão que 120 mmHg:
1,6 x 105 dina . cm-2 = (1,0 g cm-3) (980 cm s-2) (altura em cm)
Resolvendo para h, temos
h = 163 cm H2O.
EXEMPLO 9
Assuma que a área de um pé de uma pessoa de 80 kg é 25 cm x 6 cm. Determine a pressão que a pessoa exerce no chão enquanto está em pé.
SOLUÇÃO
A pressão é definida como a força por unidade de área, onde a força é o peso da pessoa W:
W = m.g = (80 kg) (9,8 m s-2) = 784 N
e a área é a área da seção transversal na qual esta força é exercida:
Apé = área de uma elipse = p (0,25 m x 0,06 m)= 0,047 m2
Desde que a pessoa normalmente fica em pé sobre os dois pés, a área total é 2 Apé = 0,094 m2. Assim, a pressão exercida pela pessoa sobre o chão é
EXEMPLO 10
Assumindo a densidade da água como 1 g/cm3, determine a pressão no fundo de uma piscina de profundidade de (1) 60 cm, (2) 120 cm e (3) 180 cm
SOLUÇÃO
Existem dois componentes de pressão atuando no fundo de uma piscina: a pressão hidrostática devida a água e a pressão atmosférica (1,0 atm = 1,013 x 105 N . m-2), assim conduzindo a uma pressão líquida ou total de
ptotal = patm + phid = patm + r . g . h
Numa profundidade de 60 cm, a pressão total exercida no fundo da piscina é
ptotal = patm + r . g . h =
1,013 x 105 N.m-2 + (1000 kg.m-3).(9,8 m.s-2).(0,6 m) =
1,07 x 105 N.m-2
Numa profundidade de 120 cm, a pressão total exercida no fundo da piscina é
ptotal = patm + r . g .h =
1,013 x 105 N.m-2 + (1000 kg.m-3) . (9,8 m.s-2) . (1,2 m) =
1,13 x 105 N.m-2
Numa profundidade de 180 cm, a pressão total exercida no fundo da piscina é:
ptotal = patm + r . g .h =
1,013 x 105 N.m-2 + (1000 kg.m-3) . (9,8 m.s-2) . (1,8 m) =
1,19 x 105 N.m-2
Veja alguns outros exemplos ilustrativos
Mais sobre a pressão no corpo humano é só clicar aqui
Veja também os efeitos fisiológicos da pressão , os efeitos da pressão durante o mergulho e a terapia com oxigênio hiperbárico (HOT).
4.1.3 – PRINCÍPIO DE PASCAL

O princípio de Pascal estabelece "uma pressão externa aplicada a um fluido confinado será transmitida igualmente a todos os pontos dentro do fluido". Isto significa que a pressão transmitida não diminui à medida que se propaga pelo interior do fluido. Este resultado torna possível uma grande multiplicação de forças, como se fosse uma alavanca fluida.
O próximo exemplo mostra melhor o que estamos dizendo.
EXEMPLO 11
Um exemplo do Princípio de Pascal é visto no macaco hidráulico, mostrado na Figura abaixo. Se uma força de 300 N é aplicada a um pistão de 1 cm2 de área transversal, determine a força de ascensão transmitida a um pistão de área transversal de 100 cm2.
SOLUÇÃO
De acordo com o Princípio de Pascal, a pressão p1 exercida na coluna da esquerda de área 1 cm2 por meio de uma força de 300 N deve ser igual a pressão p2 que aparece coluna da direita de área 100 cm2.
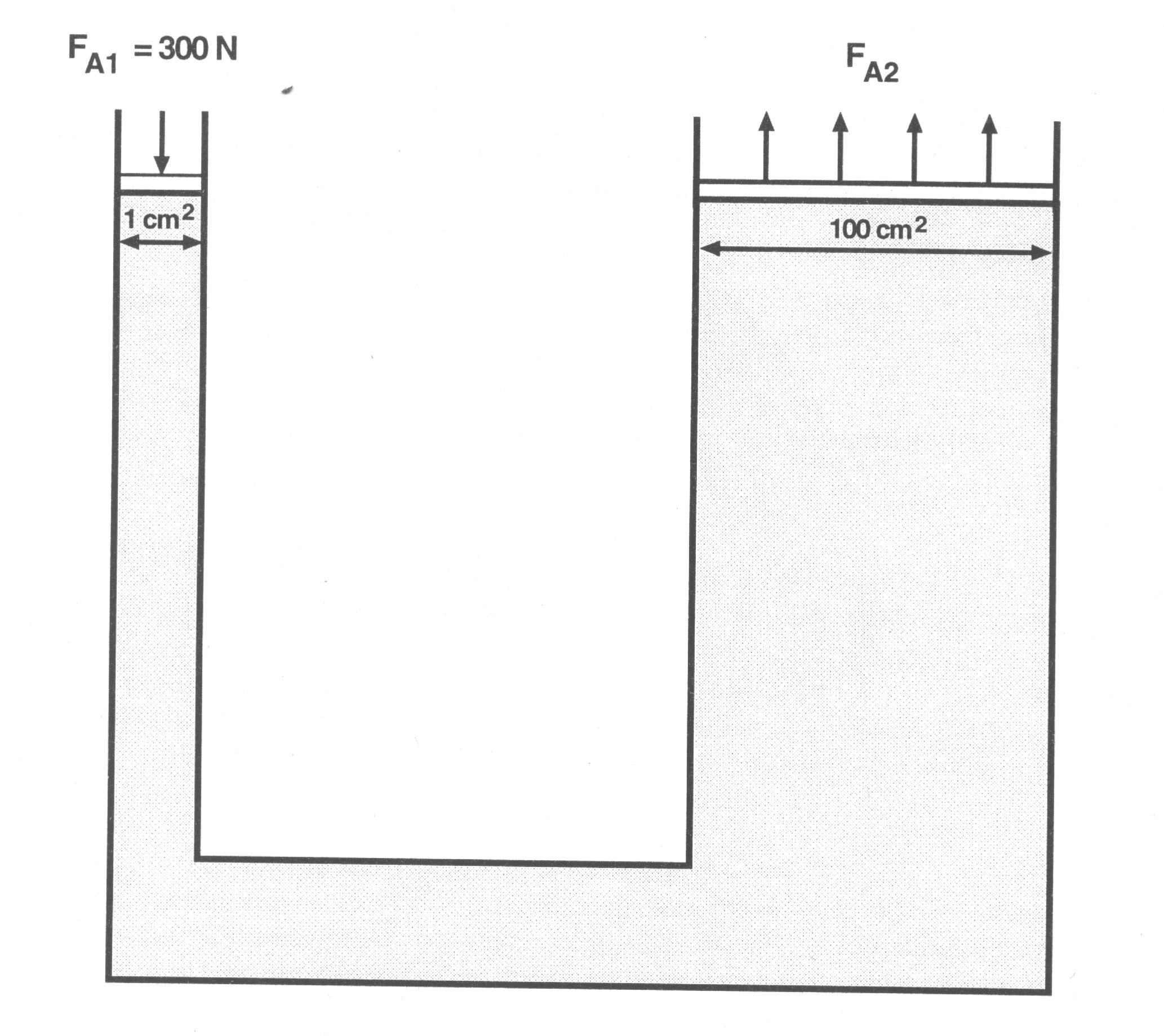
Fazendo substituições apropriadas leva
F = 30.000 N
4.1.4 – PRINCÍPIO DE ARQUIMEDES
O Princípio de Arquimedes estabelece "um corpo imerso inteiramente ou parcialmente num fluido está sujeito a um empuxo que é igual em magnitude o peso do fluido deslocado pelo corpo", ou
EMPUXO = peso do fluido deslocado
Se o empuxo é igual ou maior que o peso do fluido deslocado, então o objeto permanece flutuando. Entretanto, se o empuxo é menor que o peso do fluido deslocado, então o objeto afunda.
EXEMPLO 12
Uma baleia pesa 5,4 x 105 N. Determine o empuxo requerido para suportar a baleia no seu "habitat" natural, o oceano, quando ela está completamente submersa. Assuma que a densidade da água do mar é 1030 kg m-3 e que a densidade da baleia r baleia é aproximadamente igual a densidade da água (r água = 1000 kg m-3)
SOLUÇÃO
O volume da baleia pode ser determinado por
![]()
Resolvendo para V, temos
![]()
A baleia desloca 55,1 m3 de água quando submersa. Portanto, o empuxo E, que é igual ao peso da água deslocada, é dado por
E = Págua do mar = r água do mar . g . Vbaleia = (1030 kg m-3) (9,8 m s-2) (55,1 m3)
= 5,6 x 105 N
EXEMPLO 13
Numa atração circense, pergunta-se para estimar o número de moedas submersas num grande reservatório de água. Suponha que um reservatório de 1 litro estava cheio de moedas de massas m = 0,5 kg, tal que 0,5 litro de água fora deslocada. determine o número de moedas no reservatório, assumindo a densidade da moeda como 8,9 g cm-3
SOLUÇÃO
Dado que a massa da moeda é m = 0,5 g e a densidade é r = 8,9 g cm-3, o volume de uma única moeda é
![]()
O número de moedas é assim dado por
![]()
Dado que a massa da moeda é m = 0,5 g e a densidade é r = 8,9 g cm-3, o volume de uma única moeda é
![]()
O número de moedas é assim dado por
![]()
4.2 – TENSÃO SUPERFICIAL
A tensão superficial T é a tensão ou força por unidade de comprimento, criada por forças coesivas das moléculas na superfície de um líquido atuando para o interior. A tensão superficial é dada como a força por unidade de comprimento e é definida como a razão da força superficial F pelo comprimento d ao longo do qual a força atua, ou
A tensão superficial é dada em unidades de mN . m-1 ou dina . cm-1.
A tensão superficial da água é cerca de 72 dinas/cm.
Para mais exemplos de tensão superficial click aqui
4.3 – AÇÃO CAPILAR
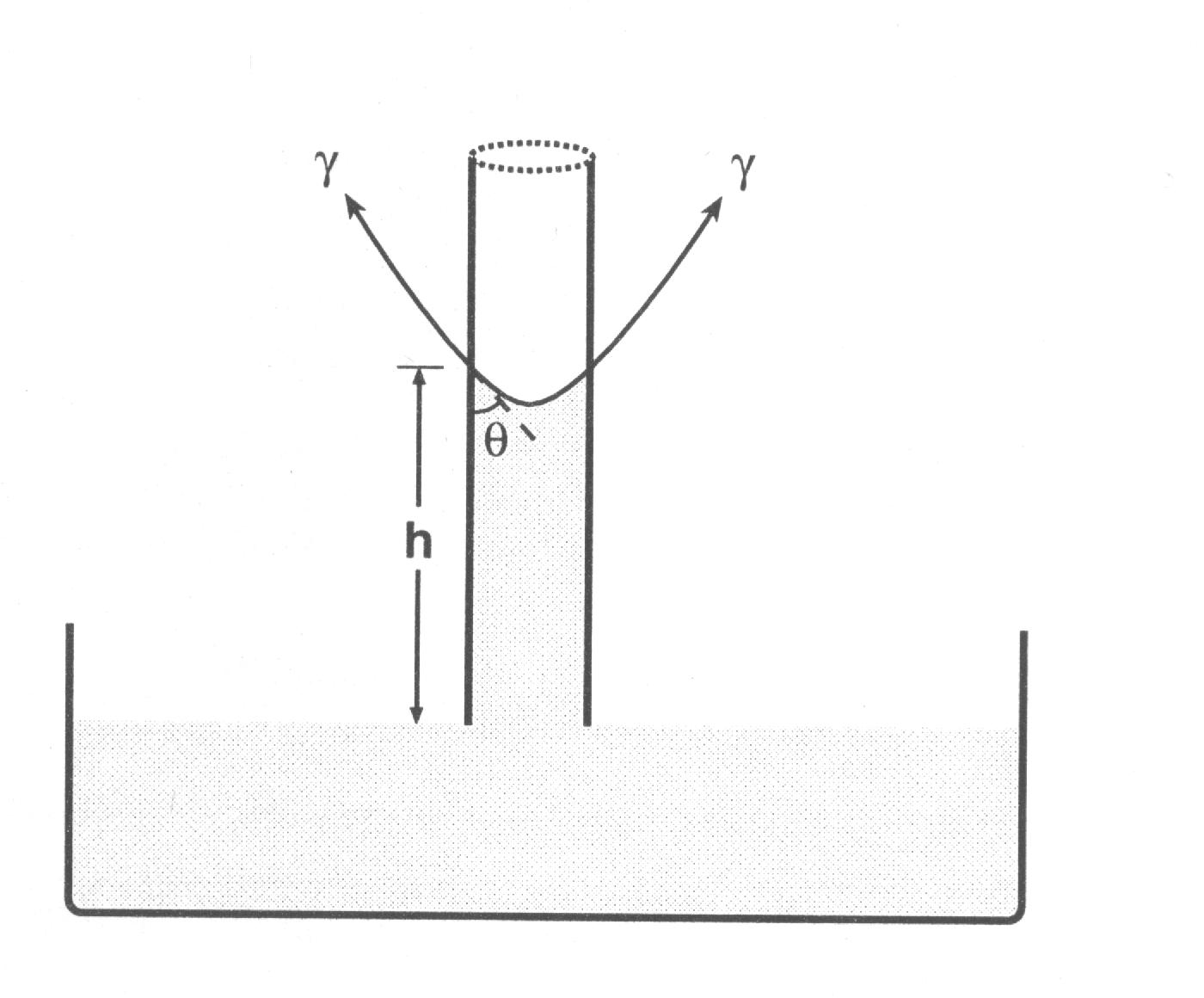
A ação capilar refere a elevação ou queda de um líquido num tubo estreito ou capilar, como mostrado na Figura abaixo, causando a formação de uma superfície curvada ou o menisco nas paredes do tubo, com a altura h dada por
onde T é a tensão superficial, q é o ângulo de contato entre a parede do capilar e a tangente à superfície do líquido e r é o raio do tubo capilar.
EXEMPLO 14
Um tubo capilar de raio interno r = 0,30 mm está parcialmente submerso em água com uma tensão superficial T = 72 dina cm-1 e um ângulo de contato q = 0º. Determine a altura de elevação da água no tubo capilar.
SOLUÇÃO
A altura h de elevação da água através do tubo capilar é
h = 4,89 cm
Se você quiser ver um exemplo ilustrativo, clique aqui
PROBLEMAS SUPLEMENTARES
Um agente anestésico tem uma densidade r = 1,86 g . cm-3 e está num tubo de ensaio de volume V = 10 ml. Determine a massa do anestésico. Resp:- 18,6 g
Dado um volume de 5 ml de álcool etílico (r = 0,81 g cm-3), determine o volume de água (r = 1,00 g cm-3) requerido para a massa igualar aquela do álcool etílico. Resp:- 4,05 ml
Determine a força exercida pela água no fundo de um tanque de aquário de 0,9 x 0,5 m se o nível de água está a 0,85 m. Resp:- 4,95 x 104 N
Determine a pressão hidrostática devida a uma coluna de 50 cm de (1) água (r água= 1 g cm-3); e 92) mercúrio (r Hg = 13,6 g cm-3). Resp:- (1) 4,9 x 104 dina cm-2; (2) 6,6 x 105 dina cm-2
Considere um barômetro de mercúrio ou um tubo de vidro de forma de U com uma extremidade ou braço lacrada e cheio de mercúrio, como mostra a Fig 4. Determine a altura h da coluna de mercúrio se a pressão no braço da extremidade aberta é (1) pressão atmosférica e (2) 100 mHg. Resp:- (1) 760 mmHg
(2) 97 mmHg
Determine a pressão hidrostática e a pressão total numa profundidade de 4,0 m numa piscina. Resp:- 3,92 x 104 N m-2; 1,4 x 105 N m-2
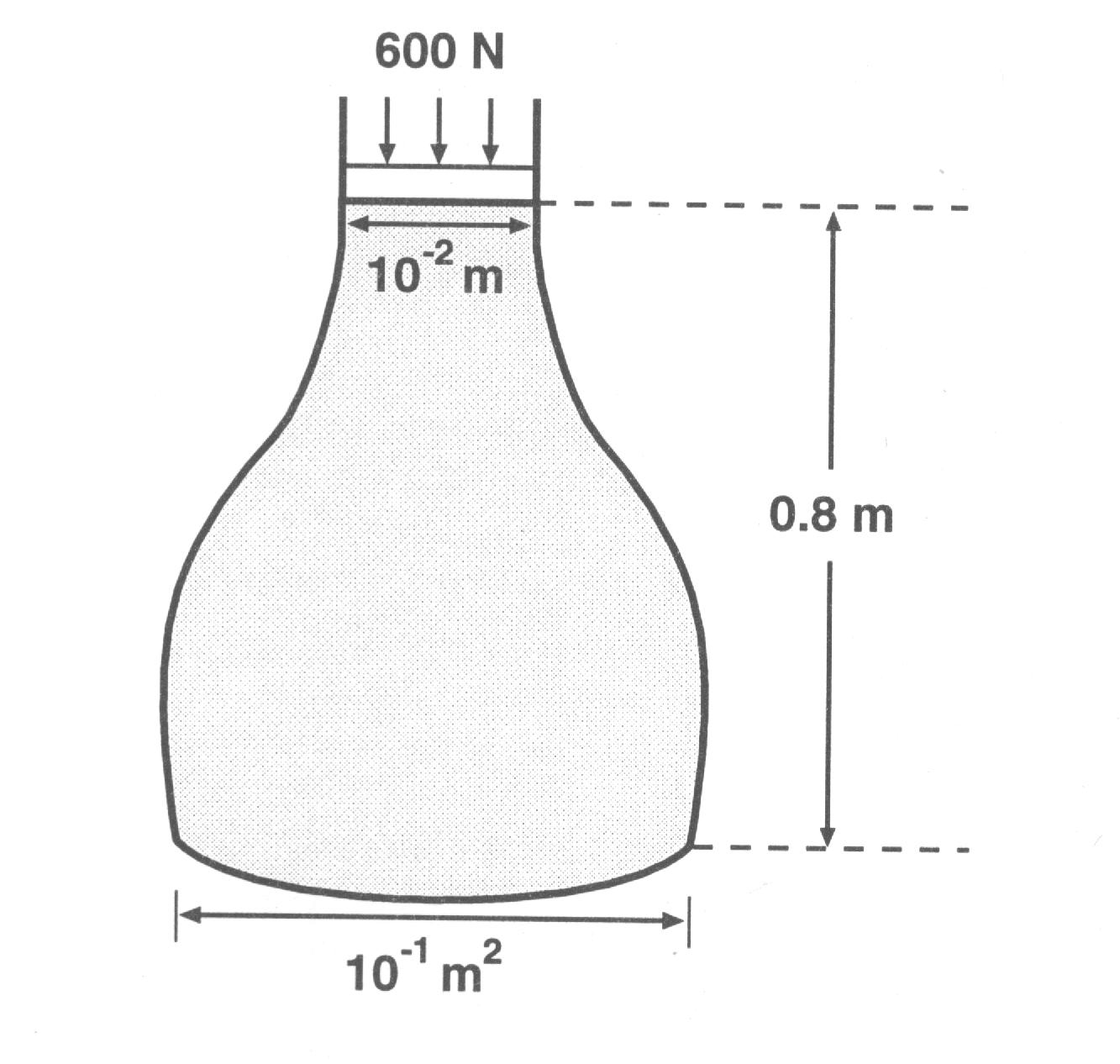
Considere um pistão de área de secção transversal 10-2 m2 exercendo uma força de 600 N num recipiente cheio de água de altura h = 0,8 m (ver Figura 5). Dada a densidade da água r = 1.000 kg m-3, determine a pressão exercida no fundo do recipiente de 10-1 m2. Resp:- 67,840 N m-2 .
Considere um cone invertido de altura h = 0,45 m e raio r = 0,15 m., cheio de água. Determine o peso e a força do fluido atuando para baixo na base do cone. Resp:- 103,8 N ; 311,6 N
Considere um tanque de aquário com uma base de 3,5 m por 2,0 m cheio de água até uma profundidade de 4 m. Determine a pressão total exercida no fundo do tanque. Resp:- 2.367 N m-2
Determine a pressão requerida para elevar água ao topo de uma construção de 20 m de altura. Resp:- 1,96 x 105 N m-2
Um aneurisma pode ser aproximado por uma esfera elástica com uma pequena abertura pela qual o sangue circula e exerce pressão contra a parede interna. determine a força, em newtons, exercida pelo sangue num aneurisma, dada uma pressão sangüínea de 150 mmHg e área de secção transversal de 25 cm2. Resp:- 49,8 N
Um tubo capilar de raio interno r = 0,2 mm está parcialmente submersa no álcool etílico. A tensão superficial e densidade do álcool etílico são 22,3 dina cm-1 e 8 x 102 kg m-3, respectivamente. Dado que o ângulo de contato é 0º, determine a altura da elevação do álcool etílico no tubo capilar. Resp:- 2,81 cm
Referindo-se ao conjunto de pistões do macaco hidráulico da Figura 3, determine a força requerida por um pistão A1 = 1 cm2 para levantar um objeto de 1.200 N sobre uma área superficial A2 = 10 cm2. Resp:- 12 N
Um tubo capilar de 1,2 mm de diâmetro interno está parcialmente submerso em água. A água eleva-se no capilar até uma altura de 18,5 mm. Dado que a densidade e a tensão superficial da água são 1,06 g cm-3 e 72,8 dina cm-1, respectivamente, determine (1) a força superficial e (2) o peso da água no tubo capilar. Resp:- 13,7 dina (2) 13,7 dina
Para uma solução num tubo de ensaio, determine a pressão, a energia potencial gravitacional Ep e a energia total Etotal em (1) no nível da superfície da solução (2) no fundo do tubo de ensaio. Resp:- (1) P = Patm; Ep = 0; Etotal = Epatm (2) P = Patm + r g h; Ep = - r g h Etotal = Patm
Para a sua viagem ao redor do mundo, Billy Bob usará um balão cheio de hélio com um volume de 2.300 m3 e um peso total de 5.500 N. Dado que a densidade do hélio é 0,176 kg m-3, determine a carga máxima que o balão pode levantar. Resp:- 1,96 x 104 N
DINÂMICA DOS FLUIDOS
Embora os fluidos difiram dos sólidos em termos de estrutura e composição, os fluidos possuem inércia, definida pela sua densidade, e estão assim sujeitos às mesmas interações físicas que os sólidos. Por exemplo, se atuado por uma força externa, os fluidos acelerarão. uma vez em movimento, os fluidos possuem energia pela qual trabalho pode ser feito. Todas estas interações dinâmicas que os fluidos em movimento possuem serão discutidas neste tópico.
Tanto na Medicina como na Biologia existem muitos fenômenos que são compreendidos através dos conceitos básicos e das propriedades de escoamento de fluidos
4.6 – DEFINIÇÕES DE ESCOAMENTO DE FLUIDOS IDEAIS
De modo geral, o escoamento de um fluido não é descrito pelo movimento individual de cada uma de suas partículas, mas é especificado por sua densidade r e velocidade de escoamento v numa determinada posição e num determinado instante
Se a velocidade v num ponto qualquer for constante em relação ao tempo, isto é, se as partículas ao passarem por aquele ponto tiverem a mesma velocidade, diz-se que o escoamento é permanente. Isto não significa que num outro ponto a velocidade não possa ser diferente.
Se a velocidade v das partículas ao passarem por um determinado ponto variar com o tempo, o escoamento é dito variado.
Se a densidade de um fluido em movimento variar, ele é considerado compressível; caso contrário, diz-se que é incompressível.
Um fluido incompressível que não apresenta resistência ao movimento chama-se fluido ideal.
A vazão Q é o volume de um fluido que passa através da seção transversal de um tubo na unidade de tempo. As suas dimensões são dadas por L3 T-1 e suas unidades são m3 s-1 ; ml s-1 ou cm3s-1.
A vazão pode também ser expressa em termos da velocidade por
Q = A . v
onde A é a área da seção transversal do tubo e v é a velocidade do fluxo.
EXEMPLO 15
Gasolina flui de uma bomba de 3,0 cm de diâmetro com uma velocidade média de 10 cm s-1. Determine a razão de fluxo da gasolina
SOLUÇÃO
A vazão está relacionada à velocidade por
Q = A.v =(p r2) v = (3,14)(1,5 cm)2 (10 cm s-1) = 70,6 cm3 s-1 = 70,6 ml s-1
EXEMPLO 16
Óleo está fluindo através de um tubo circular de raio r = 0,15 m. Se a razão de fluxo volumétrico (vazão) é medida como 0,50 m3 s-1, num certo ponto, determine:
a velocidade do óleo neste ponto e
o volume de óleo que passa neste ponto em 1 min.
SOLUÇÃO
A razão de fluxo volumétrico (ou vazão) está relacionada a velocidade por Q = A.v. Resolvendo para v e fazendo a substituição apropriada, temos
O volume do fluxo V está relacionado à vazão de fluxo volumétrico Q por
V = Q t = (0,50 m3 s-1) (60s) = 30 m3
4.7 – EQUAÇÃO DA CONTINUIDADE
A equação da continuidade estabelece que
o volume total de um fluido incompressível, isto é, fluido que mantém constante a densidade apesar das variações na pressão e na temperatura, entrando no tubo será igual aquele que está saindo do tubo e
o fluxo medido num ponto ao longo do tubo será igual ao fluxo num outro ponto ao longo do tubo, apesar da área da seção transversal do tubo em cada ponto ser diferente.
Isto pode ser expresso numa equação da forma
Q = A1 v1 = A2 v2 = constante
A equação da continuidade é uma ilustração da conservação da massa.
EXEMPLO 17
Num sistema de drenagem, uma pipa de 25 cm de diâmetro interno drena para outra pipa conectada de 22 cm de diâmetro interno. Se a velocidade da água através da pipa maior é 5 cm s-1, determine a velocidade média na pipa menor.
SOLUÇÃO
Usando a equação da continuidade, temos
A1 v1 = A2 v2
p (12,5 cm)2 (5 cm s-1) = p (11,0 cm)2 (v2)
Resolvendo para v2 dá v2 = 6,42 cm s-1.
EXEMPLO 18
Como variaria o resultado do EXEMPLO 20 se fosse usado óleo ao invés de água?
SOLUÇÃO
Não haveria alteração no resultado. A equação da continuidade é aplicável somente a fluidos que são incompressíveis, isto é, de densidade constante. O fator densidade está fora das relações entre a razão de fluxo volumétrico e velocidade de fluxo.
EXEMPLO 19
Assumindo o fluxo de um fluido incompressível, se a velocidade medida num ponto dentro de um vaso é 40 m s-1, qual é a velocidade num segundo ponto que tem um terço do raio original?
SOLUÇÃO
Este problema pode ser resolvido usando a equação da continuidade
r 1 A1 v1 = r 2 A2 v2
onde r é a densidade do sangue, A é a área da seção transversal, v é a velocidade, e os subscritos 1 e 2 referem às localizações dentro do vaso. Desde que o fluxo sangüíneo é incompressível, temos
r 1 = r 2
e v1 = 40 cm s-1, A2 = A1/3 ou A1/A2 = 3. Resolvendo para v2 dá
v2 = (A1 v1)/A2 = 3 v1 = 3 x 40 cm s-1 = 120 cm s-1
Ver o EXEMPLO ILUSTRATIVO 9
Ver o EXEMPLO ILUSTRATIVO 10
4.8 PRINCÍPIO DE BERNOULLI
O Princípio de Bernoulle, o equivalente nos fluidos à conservação da energia, estabelece que a densidade de energia de um fluxo de fluido através de um vaso rígido submetido a um gradiente de pressão, é igual à soma da densidade de energia de pressão, da densidade de energia cinética e da densidade de energia potencial gravitacional, ou
![]()
Ptotal = P + (1/2) r v2 + r g h = constante
Uma importante aplicação do Princípio de Bernoulle envolve o fluxo de fluido através de um vaso com uma região de expansão ou contração. O Princípio de Bernoulle descrevendo o fluxo de fluido através de um vaso com súbitas variações na geometria pode ser expresso como
( P + ½ r v2 + r g h)1 = (P + ½ r v2 + r g h)2
onde 1 descreve a energia do fluxo de fluido na região normal do vaso e 2 descreve a energia do fluxo de fluido na região obstruída ou alargada.
EXEMPLO 20
Expressar a lei de Bernoulle como
![]()
em termos da área transversal dos dois pontos dentro do vaso assumindo a energia potencial gravitacional igual a zero.
SOLUÇÃO
Baseado na equação da continuidade, temos
A1 v1 = A2 v2
![]()
Substituindo na expressão para o Princípio de Bernoulle, temos
![]()
EXEMPLO 21
O Princípio de Bernoulle pode ser aplicado numa seringa para descrever a dinâmica de uma injeção. Assumindo que 1 refere a posição dentro do corpo da seringa e 2 é a posição dentro do gargalo ou região anterior à entrada da agulha, derive uma expressão para a velocidade do fluido saindo do gargalo e entrando na agulha.
SOLUÇÃO
Este problema pode ser resolvido começando pelo Princípio de Bernoulle
![]()
e resolvendo para v2, temos
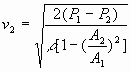
EXEMPLO 22
Qual é a energia cinética por unidade de volume de sangue que tem uma velocidade de 0,5 m s-1? (Nota: r sangue = 1.000 kg m-3.)
SOLUÇÃO
A energia cinética do sangue é dada por
Ec = ½ m v2 = ½ (r V)v2
Substituindo os valores dados no problema temos,
![]()
4.9 - TEOREMA DE TORRICELLI
O teorema de Torricelli é um caso especial do Princípio de Bernoulle e descreve a velocidade de um líquido fluindo de uma abertura num tanque cheio de líquido até uma altura h, como mostrado na Figura 5. A velocidade do lado de fora v de um líquido de uma abertura a uma distância h do nível da superfície do líquido é dado por
v =
EXEMPLO 23
Derive as bases para o Teorema de Torricelli, isto é,
v = ![]()
SOLUÇÃO
Considere um tanque cheio de água com uma abertura a uma distância h da superfície da água. A pressão da água na sua máxima altura é bastante suficiente para produzir um fluxo que sai exatamente igual ao que entra. Aplicações do Princípio de Bernoulle conduz
com o ponto 1 na superfície da água a uma altura h acima do buraco e o ponto 2 no próprio buraco
![]()
onde v é a velocidade do efluxo do buraco. Daí, resolvendo para v temos,
v = ![]()
EXEMPLO 24
Como parte de sua tarefa agrícola, Jake está enchendo um cocho com água à razão de 10-4 m s-1. Despercebido de Jake, existe um buraco circular de área transversal de 1 cm2 no cocho. Determine a altura máxima que a água atinge no cocho.
SOLUÇÃO
Este é um exemplo do Teorema de Torricelli. A velocidade de descarga do buraco é dada por
v = ![]()
No equilíbrio, v é a razão do influxo dividido pela área do buraco, ou
v = (10-4 m3 s-1) / (10-4 m2) = 1,0 m s-1
Portanto, a altura máxima da água no tanque é
h = v2/2g = (1,0 m s-1)2 / (2 x 9,8 m s-2) = 5,1 cm
PROBLEMAS SUPLEMENTARES
1. O volume de fluido fluindo
4.10 ESCOAMENTO DE FLUIDOS REAIS
O escoamento de um fluido ideal por um tubo horizontal pode ser mantido sem aplicação de forças externas, pois não existem forças dissipativas entre o fluido e o tubo, ou entre camadas adjacentes do próprio fluido. Isso, entretanto, não ocorre com fluidos reais.A viscosidade h de um fluido é uma propriedade inerente ao fluido que representa a resistência ao fluxo ou força de atrito contra o movimento do fluido ou de um objeto movendo-se nele em resposta a uma tensão de cisalhamento. A unidade SI para viscosidade é N s m-2 ou kg m-1 s-1. A viscosidade é tipicamente expressa em unidades de poise (P), onde
1 poise (P) = 0,1 kg m-1 s-1.
Colocar a Tabela 20.1 do p. 322
Todos os líquidos se tornam mais viscosos com a diminuição da temperatura. Assim, quando uma pessoa entra em estado de choque devido a um acidente, por exemplo, a temperatura de seu corpo cai; consequentemente, aumenta a viscosidade do sangue. Isso pode produzir uma queda do fluxo sangüíneo. Essa é uma das razões pelas quais as vítimas de acidentes devem ser cobertas para evitar uma diminuição grande de suas temperaturas.
4.10.1 - ESCOAMENTO LAMINAR
Uma das conseqüências da existência da viscosidade num fluido é a variação da velocidade de escoamento das camadas de fluidos. Assim as velocidades em dois pontos distintos da mesma seção transversal será diferente. Um perfil dessas velocidades pode ser obtido colocando-se um corante num líquido em escoamento. O fluido que está em contato com a parede da tubulação está em repouso, e sua velocidade aumenta com a aproximação ao eixo, onde atinge o valor máximo. A diminuição da velocidade é produzida pela força de atrito tangencial entre duas camadas adjacentes do fluido que, por sua vez, é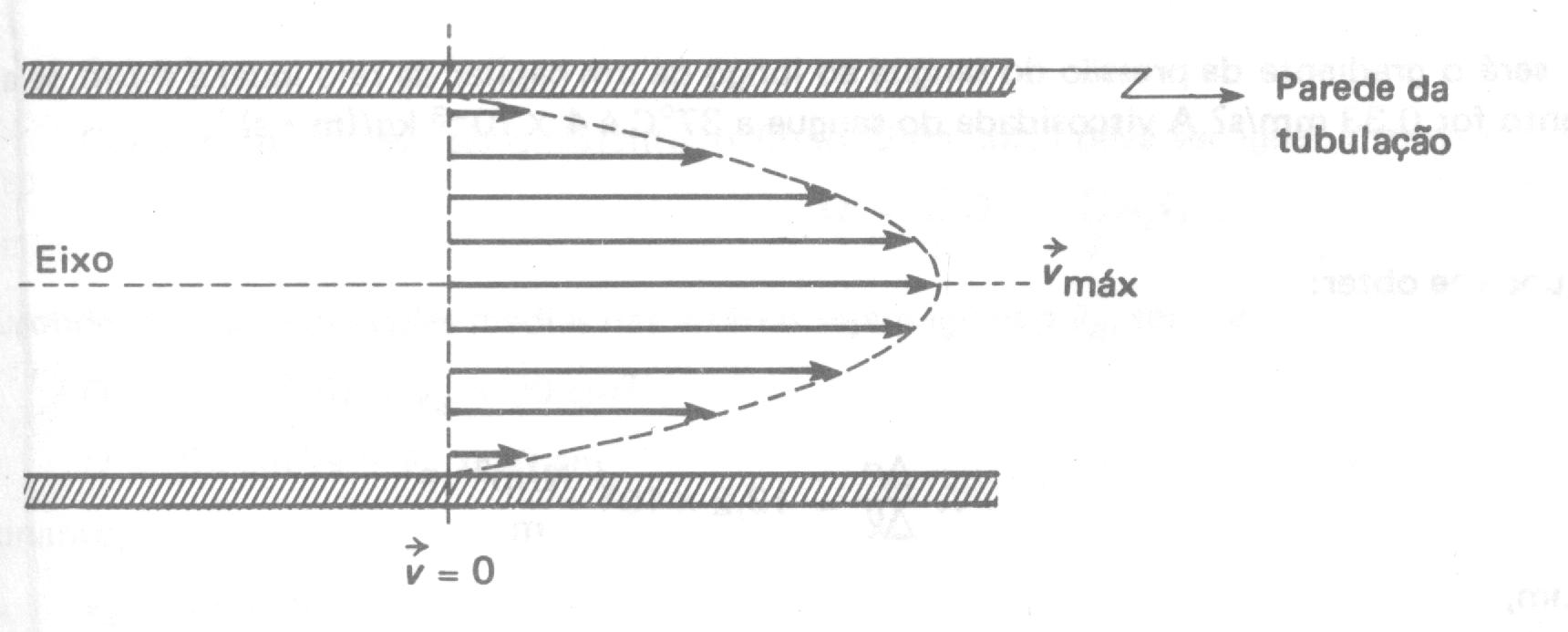
função do seu coeficiente de viscosidade.
Quando a velocidade de fluxo através de uma seção é máxima no centro e decresce segundo uma parábola até zero na camada adjacente à parede do tubo, o escoamento se diz laminar. Nesse caso, o fluxo Q de um fluido com coeficiente de viscosidade h ao longo de um tubo cilíndrico rígido de raio R e comprimento L, sujeito a um gradiente de pressão externo e constante D P pode ser expresso como
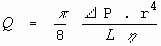
onde h é a viscosidade do fluido.Esta é a Lei de Pouseuille.
Para mais detalhes sobre a Lei de Pouseuille clique aqui
EXEMPLO 25
Determine a variação na vazão para
um decréscimo no gradiente de pressão por ½.
um acréscimo na viscosidade por 2
um decréscimo no tamanho do vaso por ½
um acréscimo no raio do vaso por 2
SOLUÇÃO
O efeito dos vários parâmetros no fluxo do fluido pode ser determinado pela análise de sua dependência qualitativa de acordo com a lei de Poiseuille:
![]()
A vazão Q é diretamente dependente do gradiente de pressão D P. Assim, um decréscimo no gradiente de pressão por 1/2 implica D P = (D P/2). Substituindo na lei de Poiseuille dá
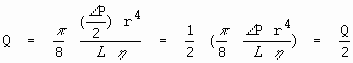
Assim, um decréscimo no gradiente de pressão por 1/2 resulta num decréscimo na vazão por 1/2.
A vazão Q é inversamente dependente da viscosidade do fluido h . Assim, um acréscimo na viscosidade do fluido por 2 implica h = 2 h
Substituindo na lei de Poiseuille, temos
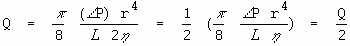
Assim, um aumento na viscosidade do fluido por 2 resulta num decréscimo na vazão por 1/2.
A vazão Q é inversamente dependente do comprimento do vaso L. Assim, um decréscimo no comprimento do vaso por 1/2 implica L = L/2
Substituindo na lei de Poiseuille, temos
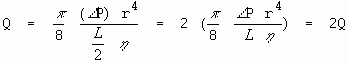
Assim, um decréscimo no comprimento do vaso pela metade resulta num acréscimo da vazão por 2.
A vazão Q é dependente do raio do vaso r à Quarta potência. assim, um acréscimo no raio do vaso por 2, implica em r = (2r)4 = 16 r4.
Substituindo na lei de Poiseuille, encontramos
![]()
Assim, um aumento no raio do vaso por 2 resulta num aumento de 16 vezes na vazão.
EXEMPLO 26
O sangue é bombeado do coração numa razão de 5 litros/min para o interior da aorta de raio 2,0 cm. Assumindo que a viscosidade e a densidade do sangue são 4 x 103 N s m-2 e 1 x 103 kg m-3, respectivamente, determine a velocidade do sangue através da aorta.
SOLUÇÃO
A velocidade de fluxo sangüíneo está relacionada à razão de fluxo volumétrico por
v = (razão de fluxo)/(área de secção transversal)
razão de fluxo = [(5 x 10-3 m3)/ min] . [1 min/60 s] = 8,33 x 10-5 m3 s-1
Área de seção transversal = p r2 = (3,14)(0,02)2 = 1,26 x 10-3 m2
Portanto, a velocidade do fluxo sangüíneo é
v = 6,6 x 10-2 m s-1 ou 6,6 cm s-1.
EXEMPLO 27
O número de vasos sangüíneos capilares na circulação humana é aproximadamente 1 x 109 com diâmetro e comprimento de cada vaso sendo 8 m m e 1 mm, respectivamente. Assumindo que a saída cardíaca é 5 litros min-1, determine:
a velocidade média do fluxo sangüíneo através dos vasos capilares,
o tempo que o sangue leva para atravessar um único vaso capilar e
o tempo requerido para 1 ml de sangue fluir através de um único vaso capilar na vazão normal.
SOLUÇÃO
A velocidade do fluxo sangüíneo através dos vasos capilares pode facilmente ser determinada por
![]()
O tempo que o sangue leva para atravessar um único vaso capilar é dado por
![]()
O tempo requerido para 1 ml de sangue fluir através de um único vaso capilar numa vazão normal é
t = (1,0 ml) / (1,66 ml s-1) = 0,60 s
Muitas vezes é conveniente escrever a Lei de Poiseuille na seguinte forma:
onde
é definida como a resistência de uma tubulação, de comprimento L e raio r, ao fluxo de viscosidade h . Essa definição continua válida mesmo para uma rede de tubos e R representa a resistência total da rede.
EXEMPLO 28
Qual será o gradiente da pressão do sangue ao longo de um capilar de raio igual a 4 m m, se a velocidade média de escoamento for 0,33 mm/s? A viscosidade do sangue a 37 ºC é 4 x 10-3 kg/(m.s)
Solução
Sabemos da Lei de Poiseuille que
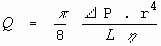
EXEMPLO 29
Qual é a vazão sangüínea através da aorta de um adulto, sabendo-se que o raio da aorta é 1 cm e a velocidade média de escoamento laminar é 0,30 m/s?
Solução
A lei de Poiseuille nos dá
![]() =
=
4.10.2 - ESCOAMENTO TURBULENTO
Em geral um fluido escoa laminarmente quando sua velocidade não é muito grande e o tubo é liso, sem protuberâncias. Entretanto, se a velocidade de fluxo atingir valores acima de certo limite (que depende de diversos fatores, como a natureza do fluido e sua temperatura), o fluido pode escoar de maneira irregular com formação de redemoinhos, resultado da mistura entre camadas adjacentes de fluido. A esse tipo de escoamento dá-se o nome de turbulento. Osborne Reynolds mostrou que, de modo geral, um escoamento por um tubo regular e retilíneo de diâmetro D deixa de ser laminar quando o número de Reynolds, definido por:
for maior que um valor crítico. Esse valor depende basicamente da natureza do fluido, do formato e da superfície interna do tubo de escoamento. Para um grande número de fluidos, seu escoamento por tubo de seção circular torna-se turbulento para  > 2.000.
A velocidade média crítica para determinado fluido que escoe numa dada tubulação, acima da qual o escoamento passa a ser turbulento é
EXEMPLO 30
O diâmetro da aorta de um adulto é da ordem de 2,2 cm. A velocidade sistólica média vsis do sangue é cerca de 60 cm/s. Considere a densidade do sangue igual à da água e sua viscosidade igual a 0,004 kg/(m.s). Determine se o fluxo do sangue na aorta é laminar ou turbulento.
Solução
O número de Reynolds dá
![]()
Portanto, o fluxo do sangue é turbulento na aorta.
Apêndice 1